MSc in Network Centered Computing

Module: PVM and MPI

PVM assignment

Background

Distributed Matrix Multiplication

Consider the example of matrix-matrix multiplication as C = AB, with A_{(l x n)}, B_{(n x m)} and C_{(l x m)}. Partition A and B into blocks as

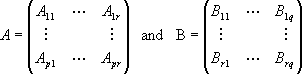
The dimension have to be compatible so that

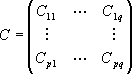
with 

is well defined.

It is reasonable to assume that all the blocks A_ik are all the same size (k₁ x k₂) and that all the blocks B_kj are all the same size (k₂ x k₃) and hence that all the blocks C_ij are all the same size (k₁ x k₃), with k₁, k₂ and k₃ not necessarily the same.
If we define the block columns

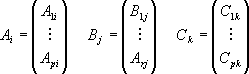
then

Then on a ring of r processors we can use the following algorithm:
LOAD PROCESSOR i:
Alocnum=I; Aloc = A(i); Bloc = B(i); Cloc = 0

FOR k = 1 TO r
     DO IN PARALLEL i = 1 TO r
          j = Alocnum;
          MULTIPLY LOCAL BLOCKS, Cloc = Cloc + Aloc * Bloc(j,i)
          SHIFT CYCLIC Aloc, Alocnmu right 1 place
     END PARALLEL
END

Where Alocnum integer indicating the column number i, Bloc(k,i) = B_ki, A(i) = A_i, B(i) = B_i, Cloc means column C_i allocated on processor i and Aloc means column A_Alocnum allocated currently on processor i. Final result is kept in block columns C_i on processor i. Thus you have to collect these block columns in order to assemble matrix C, for example in the master, in order to save and print it.

Task

[50 points]

back to the main page